
| |||||||||||||||||||||||||||||||||||||||||||||
|
(一)前言
自然界到處可見費氏數列的蹤跡,如同一樹枝上樹葉生長的距離;多數的花朵中也常見費氏數的蹤跡,百合有3瓣,金鳳花有五瓣,飛燕草常為8瓣…。費氏數也出現在向日葵的生長當中,整朵向日葵中順著兩組羅現排列,一組是順時針,另一組則為逆時針,順時針的一組數目為34,逆時針則為55,這也是費氏數中相鄰的兩項,比值也趨近黃金分割。
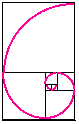
如果一個矩形的長寬比為黃金分割比例,若我們將其分成一個證方形及一和原圖相似的長方形,再由這長方形中分出一個正方形及長方形,依此類推,後我們在這些正方形中分別以這些正方形的邊長為半徑畫弧,則可以得到一條螺線,這樣子的螺線經常出現在大自然中,如螺類的殼,向日葵的花上…。 黃金分割也應用在建築上,如希臘的帕德嫩神廟、吉薩的大金字塔…。費波那西數列是學習遞迴定義一個很重要的例子,我們也往往會給學生一般式,卻忽略一般式的推導過程,所以在此介紹費波那西數列一般式的推導。 (二)費波那西數列為 (三)先備知識 (2)生成函數
(generating function): (四)推導過程 令 根據定義
從一個有趣的兔子問題揭開序幕 遞迴定義 植物世界的數學遊戲
大多數植物的花瓣數目都屬於下列這個數列3,5,8,13,21,34,55,89。
向日葵中間的筒狀花呈現出兩組螺線,一組順時針旋轉,另一組則逆時針旋轉。順時鐘方向的螺線有34條,逆時鐘方向的螺線有55條,這兩個數目恰好是費布納西數列中相鄰的兩項。螺線的數目視向日葵的種類而定,不過我們通常看到的是「34 及55」一組,或「55 及89 」一組,甚至有的是「89 及144 」一組。都恰好是費布納西數列中相鄰的兩項。雛菊也有類似的模式。 松柏的毬果有5 排鱗片向一個方向,另有3排向另一個方向;或者8排鱗片向一個方向,5排向另一個方向。 鳳梨有8排向左傾斜的鱗片,13排向右傾斜的鱗片。 這種種令人不禁驚嘆在大自然中竟隱含了這麼深刻的數學規律。這也就是費氏數列的迷人之處,關於它的研究很多,應用的範圍也十分廣泛。
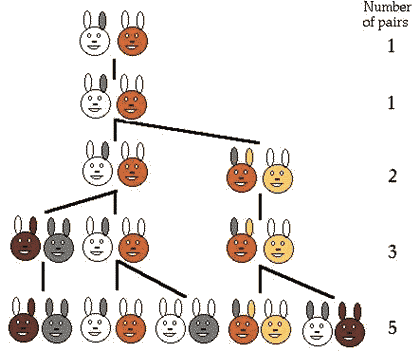
Fibonacci(1175?~1250?)是中世紀最傑出的數學家。 他原名Leonardo of Pisa,後以波那契之子而聞名。他於1175年出生於比薩,父親是個商人,很早就激發了這個小孩對算術的興趣。他們旅行到西西里,埃及和敘利亞,實際上接觸到阿拉伯的數學歷練。 Fibonacci很快就發現了十進位數字系統的好處,在數字及計算上比當時通行的但十分笨拙的羅馬數字系統優越得太多。1202年,他回到家鄉,發表了著名的《算盤書》,將阿拉伯數字系統引進歐洲,立刻大受歡迎,並且很快地流傳開來,不久便取代了羅馬數系。 這本書共十五章,包括了阿拉伯數字的寫法與讀法,整數及分數的計算,平方根與立方根的計算,用試位法及代表解法解線性及二次方程等等。書中包含了許多問題,其中又以「兔子問題」最為有名: 一對兔子,每月生一對小兔子,新生的小兔子過了兩個月以後又開始生小兔子,問:一對兔子一年能繁殖多少兔子? 根據題意,以Fn表示個月以後兔子的總對數,則F1=1,F2=1,F3=2,F4=3,F5=5,F6=8,F7=13,F8=21,…,這個數列就叫作Fibonacci數列(或稱費氏數列),引起了後世源源不斷的興趣。Fibonacci數列有下列表達式:
費氏數列與黃金分割 費氏數列的模式在自然界及數學的許多地方一再地出現,內容豐富而美麗,這是它深具興味的理由。 Fibonacci觀察兔子的繁殖現象,在1202年提出今日所謂的費氏數列。有些花草或樹木,其枝幹之分枝成長也符合費氏數列的模式。更令人驚奇的是,費氏數列竟然出現在雄蜜蜂的家譜之中。在蜜蜂的王國,女王蜂產卵孵化成雄蜂,受精的卵孵化成工蜂或女王蜂,因此雄蜂只有母親沒有父親。考慮一隻雄蜂的家譜,牠的歷代祖先之個數成為費氏數列,並且第七代的十三位祖先恰好可以排列成鋼琴八度音的十三個半音階(八個白鍵,五個黑鍵)。 所謂黃金分割就是將一個線段分割成大小兩段,使得 全段:大段=大段:小段 若令全段為1,大段為x,則小段為1-x,從而
西元 1509年Luca Pacioli( 1445~1517)寫了一本書「De Divina Proportione 」,首先稱它做「黃金比率」(golden ratio),Luca Pacioli 是文藝復興時代畫家巨匠達文西的摯友,達文西的畫作就經常運用黃金比率0.618,如「蒙納麗莎的微笑」和達文西自畫像。自此 在美學與建築上,寬長之比約為0.618的矩形被認為是最和諧, 最合乎美的造型。 德國心理學家古斯塔夫‧費希納(1801~1887)和伍得特(1832~1920)把黃金矩形(寬長比率約為0.618)當成科學心理學這個新領域中首批研究的對象之一。1876年,他們將10個不同比例的白色矩形擺放在一張黑色的桌子上,問受試者哪一個從美學角度講看起來最令人舒服。35%的受試者表示喜歡邊長比符合黃金比率的矩形。40%的受試者選擇了趨近於這個比率的矩形。而沒有任何人將黃金比率選作是最不喜歡的比率。之後,費希納又測量了22家博物館和藝術長廊的2萬張畫,收集了數據, 但是發現黃金比率並不和這些名畫的高、寬比率有絕對相關。雖然費希納實驗後的150年裡,沒有人支持觀點同意黃金矩形是最合乎美的矩形,同時也沒有人能提供確鑿的證據解釋為什麼它更好。但是,同時一些人卻堅持認為,雖然沒有足夠的理論證據,但是黃金比率確實真實存在於自然界裡,而且是最和諧也是合乎美學的比率。 就如普通樹葉的寬與長之比,蝴蝶身長與雙翅展開後的長度之比也接近0.618。如果以牛馬虎的前肢為界作一垂直虛線,將軀體分為兩部分,其水平長度之比恰符合黃金比率。通常我們在環境溫度為22℃~24℃時能有最舒適的感覺,身體的新陳代謝、生理節奏和機能可處在最佳狀態。而人體的正常體溫為37℃,它和0.618的相乘積正好是22℃。醫學專家也觀察到,人在精神愉快時的腦電波頻率下限是8赫茲,而上限是12.9赫茲,上下限的比率接近於0.618,如果我們在這時參加基本學力測驗,一定會有更好的表現。此外,我們正常血壓的舒張壓與收縮壓的比例關係;我們正常睡眠時間與活動時間的比例關係,都足以說明黃金比率扮演和諧美滿的角色是無所不在的。 歐洲 中世紀的物理學家、天文學家家科卜勒(J.Kepler1571-1630)對黃金分割做了很高的評價,他說:「幾何學有兩大寶藏,一個是畢氏定理;另一個是黃金分割。前者是金礦,而後者是珍貴的鑽石礦」。 目前,我們看的書、報、雜誌,其紙張的裁切寬與長之比就接近黃金比率。這樣的矩形讓人看起來舒服,被稱為「黃金矩形」。原為黃金矩形的紙張,對折後仍是黃金矩形。如8開、16開、32開等,都近似於的黃金矩形。 古埃及的金字塔,形似方錐,大小雖有不同,但是金字塔底面的邊長與高的比率都接近於0.618。而近代著名的法國巴黎埃費爾鐵塔,其第二層以下和第二層以上的高度比率是0.618。目前世界最高的建築物是加拿大多倫多電視塔,高553.33
| |||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||

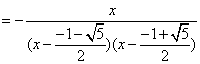
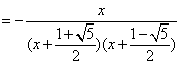





 費波那契(Fibonacci, Leonardo)
費波那契(Fibonacci, Leonardo)
